Matrix and Graph

บทความนี้จะอธิบายเรื่อง Matrix รวมถึงการนำ Matrix ไปใช้กับปัญหาด้าน Graph เริ่มต้นจาก Matrix ก็คือตารางที่มีข้อมูลอยู่ภายใน เช่น Matrix ขนาด 3 x 4 คือมี 3 Rows และ 4 Columns

		8.5  7.8  7.9  7.5  Row 0
		8.3  7.9  8.1  7.7  Row 1
		7.9  8.0  8.2  7.8  Row 2
Column    0    1    2    3

ใน Row แรกมีข้อมูลคือ 8.5, 7.8, 7.9, 7.5 ตามลำดับ ใน Row แรก เรียกว่า Row ที่ 0
ใน Column แรก มีข้อมูลคือ 8.5, 8.3, 7.9 ใน Column แรกเรียกว่า Column ที่ 0 เหมือนกัน
จาก Matrix ข้างบนเขียนเป็นภาษา Java ได้ 2 แบบ คือแบบจองพื้นที่ไว้ก่อน และ แบบใส่ข้อมูลไปทันที เช่น

double[][] a = new double[3][4];
a[0][0] = 8.5;
a[0][1] = 7.8;
a[0][2] = 7.9;
...
a[2][3] = 7.8;

หรือ

double[][] b =  {
					{8.5, 7.8, 7.9, 7.5},
					{8.3, 7.9, 8.1, 7.7},
					{7.9, 8.0, 8.2, 7.8}
				};

Matrix อาจจะเรียกว่า 2-Dimensional Array หรือ Array แบบ 2 มิติก็ได้ จำนวน Row ของ Matrix b หาได้จาก b.length ส่วนจำนวน Column หาได้จาก b[0].length แต่ละ Row อาจจะมีจำนวน Column ไม่เท่ากันก็ได้ เรียกว่า Jagged Array
ตัวอย่าง การพิมพ์ข้อมูลใน Column แรก

double[][] a = new double[3][4];
for (int i = 0; i < a.length; i++) {
	System.out.println(a[i][0]);
}

ตัวอย่าง การพิมพ์ข้อมูลใน Matrix

double[][] a = new double[3][4];
for (int i = 0; i < a.length; i++) {
	for (int j = 0; j < a[i].length; j++) {
		System.out.print(a[i][j] + " ");
	}
	System.out.println();
}

แบบฝึกหัด ให้เขียน Code พิมพ์ Matrix ของจำนวนเต็ม และ หาผลรวมแต่ละ Row เช่น

int[][] m = {
				{ 3, 4, 2, 5},
				{ 2, 1, 6, 4},
				{ 2, 3, 1, 0}
			};

ผลลัพธ์

	3  4  2  5    = 14
	2  1  6  4    = 13
	2  3  1  0    =  6

แบบฝึกหัด ให้เขียน Code พิมพ์ Matrix ของจำนวนเต็ม แล้ว หาผลรวมแต่ละ Column เช่น

int[][] m = {
				{ 3, 4, 2, 5},
				{ 2, 1, 6, 4},
				{ 2, 3, 1, 0}
			};

ผลลัพธ์

แบบฝึกหัด ให้เขียน Code เพื่อ Transpose Matrix แบบจตุรัส เช่น

1 2 3 4 5          1 6 3 4 9
6 7 8 9 0          2 7 2 3 8
3 2 4 1 7     =>   3 8 4 1 3
4 3 1 2 9          4 9 1 2 4
9 8 3 4 3          5 0 7 9 3

แบบฝึกหัด ให้เขียน Code หาว่า Matrix แบบจตุรัส เป็นสมมาตร หรือ Symmetry ใน Main Diagonal จากบนซ้ายไปล่างขวา หรือไม่ เช่น

1 2 3 4         1 0 0 0          1
2 7 6 8         1 1 0 0          Symmetry
3 6 5 9         1 1 1 0
4 8 9 2         1 1 1 1
Symmetry        Asymmetry

Graph

ตัวอย่างของ Graph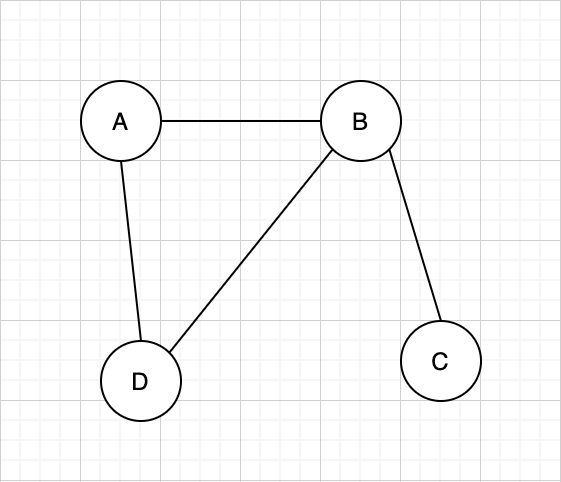

จากภาพ Vertex คือ A, B, C, D
Edge เป็นคู่ลำดับของ Vertex จากภาพ มี Edge คือ

(A,B)
(A,D)
(B,C)
(B,D)

Graph ประกอบด้วย Vertex และ Edge จาก Graph ข้างบน G = (V,E) คือ

G = (V, E)
  = ( { A, B, C, D }, { (A,B), (A,D), (B,C), (B,D) } )

ถ้ามี Edge จาก A -> B นั่นคือจะมี Edge จาก B -> A ด้วย
Directed Graph คือ Graph ที่มีลูกศร เช่น ถ้ามี Edge จาก A -> B ไม่ได้หมายความว่ามี Edge จาก B -> A หนังสือบางเล่มจะเรียก Directed Graph ว่า Digraph
Weighted Graph คือ Graph ที่มีน้ำหนัก เช่น

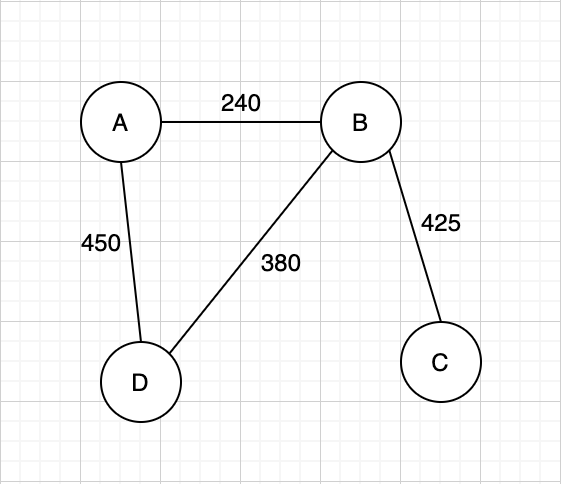
Graph สามารถเก็บไว้ใน File ข้อมูลได้ เช่น

A B
A D
B C
B D

หรือ

A B 240
A D 450
B C 425
B D 380

Matrix สามารถใช้เก็บ Graph ได้ เช่นใช้ Adjacency Matrix เพื่อเก็บความสัมพันธ์ระหว่าง Vertex กับ Vertex ตัวอย่างการเก็บ Graph และ Weighted Graph

   A  B  C  D               A    B    C    D
A     1     1           A       240       450
B  1     1  1           B  240       425  380
C     1                 C       425
D  1  1                 D  450  380

ปัญหาตอนนี้คือใน File ยังไม่รู้จำนวน Vertex ทำให้ยังจองพื้นที่ไม่ได้ ดังนั้น File ข้อมูลต้องเพิ่มจำนวน Vertex เข้าไปด้วย เช่น

4
A B
A D
B C
B D

ตัวอย่าง การเขียน Code อ่านข้อมูลจาก File แล้วสร้าง Matrix

import java.io.*;
import java.util.*;
class Start {
	public static void main(String[] z) {
		try {
			File file = new File("graph-1.txt");
			Scanner in = new Scanner(file);
			int vertex = in.nextInt();
			int[][] matrix = new int[vertex][vertex];
			while (in.hasNext()) {
				String source = in.next();
				String target = in.next();
				char s = source.charAt(0);
				char t = target.charAt(0);
				matrix[s-'A'][t-'A'] = 1;  // A => B
				matrix[t-'A'][s-'A'] = 1;  // B => A
			}
		} catch (Exception e) { }
	}
}